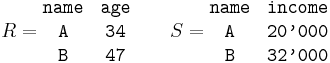Information algebra
Classical information theory goes back to Claude Shannon. It is a theory of information transmission, looking at communication and storage. However, it has not been considered so far that information comes from different sources and that it is therefore usually combined. It has furthermore been neglected in classical information theory that one wants to extract those parts out of a piece of information that are relevant to specific questions.
A mathematical phrasing of these operations leads to an algebra of information, describing basic modes of information processing. Such an algebra grasps a lot of formalisms of computer science, which seem to be different on the surface: relational databases, multiple systems of formal logic or numerical problems of linear algebra. It allows the development of generic procedures of information processing and thus a unification of basic methods of computer science, in particular of distributed information processing.
Contents |
Information algebra
Information relates to precise questions, comes from different sources, must be aggregated and can be focused on questions of interest. Starting from these considerations, information algebras (Kohlas 2003) are two-sorted algebras 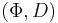 , where
, where 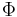 is a semigroup, representing combination or aggregation of information,
is a semigroup, representing combination or aggregation of information, 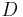 is a lattice of domains (related to questions) whose partial order reflects the granularity of the domain or the question, and a mixed operation representing focusing or extraction of information.
is a lattice of domains (related to questions) whose partial order reflects the granularity of the domain or the question, and a mixed operation representing focusing or extraction of information.
Information and its operations
More precisely, in the two-sorted algebra 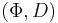 , the following operations are defined
, the following operations are defined
|
Additionally, in 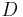 the usual lattice operations (meet and join) are defined.
the usual lattice operations (meet and join) are defined.
Axioms and definition
The axioms of the two-sorted algebra 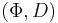 , in addition to the axioms of the lattice
, in addition to the axioms of the lattice 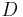 :
:
To focus an information on
To focus an information on
An information combined with a part of itself gives nothing new.
Each information refers to at least one domain (question). |
A two-sorted algebra 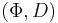 satisfying these axioms is called an Information Algebra.
satisfying these axioms is called an Information Algebra.
Order of information
A partial order of information can be introduced by defining 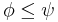 if
if 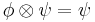 . This means that
. This means that 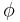 is less informative than
is less informative than 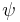 if it adds no new information to
if it adds no new information to 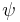 . The semigroup
. The semigroup 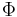 is a semilattice relative to this order, i.e.
is a semilattice relative to this order, i.e. 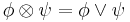 . Relative to any domain (question)
. Relative to any domain (question) 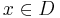 a partial order can be introduced by defining
a partial order can be introduced by defining 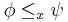 if
if 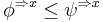 . It represents the order of information content of
. It represents the order of information content of 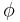 and
and 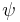 relative to the domain (question)
relative to the domain (question) 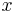 .
.
Labeled information algebra
The pairs 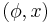 , where
, where 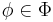 and
and 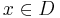 such that
such that 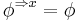 form a labeled Information Algebra. More precisely, in the two-sorted algebra
form a labeled Information Algebra. More precisely, in the two-sorted algebra 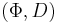 , the following operations are defined
, the following operations are defined
|
Models of information algebras
Here follows an incomplete list of instances of information algebras:
- Relational algebra: The reduct of a relational algebra with natural join as combination and the usual projection is a labeled information algebra, see Example.
- Constraint systems: Constraints form an information algebra (Jaffar & Maher 1994).
- Semiring valued algebras: C-Semirings induce information algebras (Bistarelli & Montanari Rossi1997);(Bistarelli et al. Schiex);(Kohlas & Wilson 2006).
- Logic: Many logic systems induce information algebras (Wilson & Mengin 1999). Reducts of cylindric algebras (Henkin, Monk & Tarski 1971) or polyadic algebras are information algebras related to predicate logic (Halmos 2000).
- Module algebras: (Bergstra, Heering & Klint 1990);(de Lavalette 1992).
- Linear systems: Systems of linear equations or linear inequalities induce information algebras (Kohlas 2003).
Worked-out example: relational algebra
Let 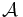 be a set of symbols, called attributes (or column names). For each
be a set of symbols, called attributes (or column names). For each 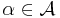 let
let 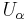 be a non-empty set, the set of all possible values of the attribute
be a non-empty set, the set of all possible values of the attribute 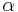 . For example, if
. For example, if 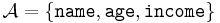 , then
, then 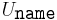 could be the set of strings, whereas
could be the set of strings, whereas 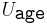 and
and 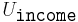 are both the set of non-negative integers.
are both the set of non-negative integers.
Let 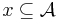 . An
. An 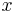 -tuple is a function
-tuple is a function 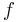 so that
so that 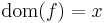 and
and 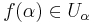 for each
for each 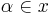 The set of all
The set of all 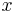 -tuples is denoted by
-tuples is denoted by 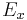 . For an
. For an 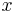 -tuple
-tuple 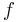 and a subset
and a subset 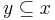 the restriction
the restriction ![f[y]\,](/2012-wikipedia_en_all_nopic_01_2012/I/6c74ba5233291f8e9b56aa28099c5e93.png) is defined to be the
is defined to be the 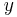 -tuple
-tuple 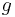 so that
so that  for all
for all 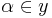 .
.
A relation 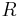 over
over 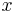 is a set of
is a set of 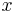 -tuples, i.e. a subset of
-tuples, i.e. a subset of 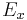 . The set of attributes
. The set of attributes 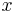 is called the domain of
is called the domain of 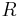 and denoted by
and denoted by 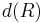 . For
. For 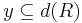 the projection of
the projection of 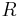 onto
onto 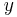 is defined as follows:
is defined as follows:
The join of a relation 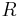 over
over 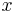 and a relation
and a relation 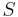 over
over 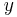 is defined as follows:
is defined as follows:
As an example, let 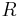 and
and 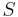 be the following relations:
be the following relations:
Then the join of 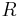 and
and 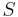 is:
is:
A relational database with natural join 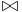 as combination and the usual projection
as combination and the usual projection 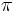 is an information algebra. The operations are well defined since
is an information algebra. The operations are well defined since
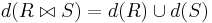
- If
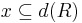 , then
, then 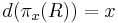 .
.
It is easy to see that relational databases satisfy the axioms of a labeled information algebra:
- semigroup
 and
and 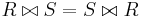
- transitivity
- If
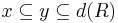 , then
, then 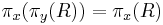 .
. - combination
- If
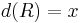 and
and 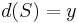 , then
, then 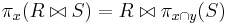 .
. - idempotency
- If
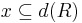 , then
, then 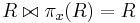 .
. - support
- If
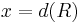 , then
, then 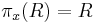 .
.
Connections
- Valuation algebras
- Dropping the idempotency axiom leads to Valuation Algebras. These axioms have been introduced by (Shenoy & Shafer 1990) to generalize local computation schemes (Lauritzen & Spiegelhalter 1988) from Bayesian networks to more general formalisms (including belief function, possibility potentials, etc.) (Kohlas & Shenoy 2000).
- Domains and information systems
- Compact Information Algebras (Kohlas 2003) are related to Scott domains and Scott information systems (Scott 1970);(Scott 1982);(Larsen & Winskel 1984).
- Uncertain information
- Random variables with values in information algebras represent probabilistic argumentation systems (Haenni, Kohlas & Lehmann 2000).
- Semantic information
- Information algebras introduce semantics by relating information to questions through focusing and combination (Groenendijk & Stokhof 1984);(Floridi 2004).
- Information flow
- Information algebras are related to information flow, in particular classifications (Barwise & Seligman 1997).
- Tree decomposition
- ...
- Semigroup theory
- ...
Historical Roots
The axioms for information algebras are derived from the axiom system proposed in (Shenoy and Shafer, 1990), see also (Shafer, 1991).
References
- Barwise, J.; Seligman, J. (1997), Information Flow: The Logic of Distributed Systems, Cambridge U.K.: Number 44 in Cambridge Tracts in Theoretical Computer Science, Cambridge University Press
- Bergstra, J.A.; Heering; Klint, P. (1990), "Module algebra", J. of the assoc. for Computing Machinery 73 (2): 335–372
- Bistarelli, S.; Fargier, H.; Montanari, U.; Rossi, F.; Schiex, T.; Verfaillie (1999), "Semiring-based CSPs and valued CSPs: Frameworks, properties, and comparison", Constraints 4 (3): 199–240, ftp://ftp.irit.fr/pub/IRIT/RPDMP/PapersFargier/valuatedItaliens.ps.gz
- Bistarelli, Stefano; Montanari, Ugo; Rossi, Francesca (1997), "Semiring-based constraint satisfaction and optimization", Journal of the ACM 44 (2): 201–236, ftp://ftp.di.unipi.it/pub/Papers/rossi/jacm.ps.gz
- de Lavalette, Gerard R. Renardel (1992), "Logical semantics of modularisation", in Egon Börger, Gerhard Jäger, Hans Kleine Büning, and Michael M. Richter, CSL: 5th Workshop on Computer Science Logic, Volume 626 of Lecture Notes in Computer Science, Springer, pp. 306–315, ISBN 3-540-55789-X, http://citeseer.ist.psu.edu/484529.html
- Floridi, Luciano (2004), "Outline of a theory of strongly semantic information", Minds and Machines 14 (2): 197–221
- Groenendijk, J.; Stokhof, M. (1984), Studies on the Semantics of Questions and the Pragmatics of Answers, PhD thesis, Universiteit van Amsterdam
- Haenni, R.; Kohlas, J.; Lehmann (2000), "Probabilistic argumentation systems", in J. Kohlas and S. Moral, Handbook of Defeasible Reasoning and Uncertainty Management Systems, Dordrecht: Volume 5: Algorithms for Uncertainty and Defeasible Reasoning, Kluwer, pp. 221–287, http://diuf.unifr.ch/tcs/publications/ps/hkl2000.pdf
- Halmos, Paul R. (2000), "An autobiography of polyadic algebras", Logic Journal of the IGPL 8 (4)
- Henkin, L.; Monk, J. D.; Tarski, A. (1971), Cylindric Algebras, Amsterdam: North-Holland, ISBN 0-7204-2043-1
- Jaffar, J.; Maher, M. J. (1994), "Constraint logic programming: A survey", J. of Logic Programming 19/20: 503–581
- Kohlas, J. (2003), Information Algebras: Generic Structures for Inference, Springer-Verlag, ISBN 1852336897
- Kohlas, J.; Shenoy, P.P. (2000), "Computation in valuation algebras", in J. Kohlas and S. Moral, Handbook of Defeasible Reasoning and Uncertainty Management Systems, Volume 5: Algorithms for Uncertainty and Defeasible Reasoning, Dordrecht: Kluwer, pp. 5–39
- Kohlas, J.; Wilson, N. (2006), Exact and approximate local computation in semiring-induced valuation algebras, Technical Report 06-06, Department of Informatics, University of Fribourg, http://diuf.unifr.ch/tcs/publications/ps/kohlaswilson06.pdf
- Larsen, K. G.; Winskel, G. (1984), "Using information systems to solve recursive domain equations effectively", in Gilles Kahn, David B. MacQueen, and Gordon D. Plotkin, Semantics of Data Types, International Symposium, Sophia-Antipolis, France, June 27–29, 1984, Proceedings, 173 of Lecture Notes in Computer Science, Berlin: Springer, pp. 109–129
- Lauritzen, S. L.; Spiegelhalter, D. J. (1988), "Local computations with probabilities on graphical structures and their application to expert systems", J. Royal Statis. Soc. B 50: 157–224
- Scott, Dana S. (1970), Outline of a mathematical theory of computation, Technical Monograph PRG–2, Oxford University Computing Laboratory, Programming Research Group
- Scott, D.S. (1982), "Domains for denotational semantics", in M. Nielsen and E.M. Schmitt, Automata, Languages and Programming, Springer, pp. 577–613
- Shafer, G. (1991), An axiomatic study of computation in hypertrees, Working Paper 232, School of Business, University of Kansas
- Shenoy, P. P.; Shafer, G. (1990), Axioms for probability and belief-function proagation, in Ross D. Shachter, Tod S. Levitt, Laveen N. Kanal, and John F. Lemmer, "Uncertainty in Artificial Intelligence 4", Machine intelligence and pattern recognition (Amsterdam: Elsevier) 9: 169–198, ISBN 0-444-88650-8
- Wilson, Nic; Mengin, Jérôme (1999), "Logical deduction using the local computation framework", in Anthony Hunter and Simon Parsons,, Symbolic and Quantitative Approaches to Reasoning and Uncertainty, European Conference, ECSQARU’99, London, UK, July 5–9, 1999, Proceedings, volume 1638 of Lecture Notes in Computer Science, Springer, pp. 386–396, ISBN 3-540-66131-X, http://springerlink.metapress.com/openurl.asp?genre=article&issn=0302-9743&volume=1638&spage=0386
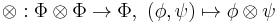
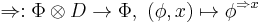
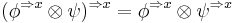
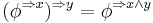
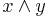 .
.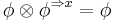
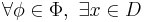 such that
such that 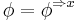
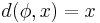

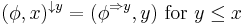
![\pi_y(R):=\{f[y]\mid f\in R\}.\,](/2012-wikipedia_en_all_nopic_01_2012/I/28bc9b3f7eb54ac6f0700213a3cc5854.png)
![R\bowtie S:=\{f\mid f \quad (x\cup y)\hbox{-tuple},\quad f[x]\in R,
\;f[y]\in S\}.\,](/2012-wikipedia_en_all_nopic_01_2012/I/8dbf05413e9513f7779f1e793657188a.png)